第一章 基础
1. 一般步骤:
- 得到一个有限训练集(Date Set)
- 确定假设空间(学习模型的集合Model Set)
- 确定模型的选择准则(学习策略Strategy)
- 实现求解最优化模型的算法(Algotithm)
- 通过学习方法选择最有模型
- 利用学习的最优模型对新数据集进行预测或分析


2. 模型
2.1 非概率模型
- 参数向量$ \theta \in \mathbf{R}^n $决定的函数族:
2.2 概率模型
3. 策略
3.1 损失函数或风险函数
- $ \text{0-1}\ Loss\ Function $
\[
L(Y,f(X)) =
\begin{cases}
1, &\text{$Y \ne f(X)$}\\\
0, &\text{$Y=f(X)$}
\end{cases} \tag{5}
\]
- $ Quadratic\ Loss\ Function $
\[
L(Y,f(X)) = (Y-f(X))^2 \tag{6}
\]
- $ Absolute\ Loss\ Function $
\[
L(Y,f(X)) = |Y-f(X)| \tag{7}
\]
- $ Logarithmic\ Loss\ Function\ or\ \text{log-likelihood}\ Loss\ Function $
\[
L(Y,P(Y|X)) = -logP(Y|X) \tag{8}
\]
- $ Risk\ Function\ or\ Expected\ Loss $
\[
R_{exp}(f)=E_p[L(Y,P(Y|X))]= \int_\{x \times y\} L(y,f(x))P(x,y)dxdy \tag{9}
\]
联合分布$ P(X,Y) $未知, $ R_{exp}(f) $不能直接计算.
- $ Empirical\ Risk\ or\ Empirical\ Loss $
\[
R_{emp}(f)=\frac{1}{N} \sum_{i=1}^{N}L(y_i,f(x_i)) \tag{10}
\]
期望风险$ R_{exp}(f) $是模型关于联合分布的期望损失, 经验风险$ R_{emp}(f) $是模型关于训练样本集的平均损失.
根据大数定律 $ \lim_{N\to\infty}R_{emp}=R_{exp} $.可用经验风险估计期望风险.
\[
min_{f \in \mathscr{F}}R_{emp}(f)=min_{f \in \mathscr{F}}\frac{1}{N} \sum_{i=1}^{N}L(y_i,f(x_i)) \tag{11}
\]
当样本容量足够大,经验风险最小化能保证很好的学习效果,如MLE$ 极大似然估计(Maximum\ Likelihood\ Estimation) $.
当模型是条件概率分布,损失函数是对数函数时,经验风险最小化(EMP)等价于极大似然估计(MLE).
但是,当样本容量很小时,会产生过拟合(over-fitting)现象.于是,为了防止过拟合,可采用结构风险最小化(Structural Risk Minimization,SRM).
- $ Structural\ Risk\ or\ Structural\ Loss $
\[
R_{srm}(f)=\frac{1}{N} \sum_{i=1}^{N}L(y_i,f(x_i)) + \lambda J(f) \tag{12}
\]
结构风险在经验风险上加上表示模型复杂度的正则化项(regularizer)或罚项(penalty term).
结构风险最小化(SRM)等价于正则化(Regularization).
$ J(f) $为模型的复杂度,是定义在假设空间$ \mathscr{F} $上的泛函.模型越复杂,复杂度越大,复杂度一定意义上表示了对复杂模型的惩罚.
\[
min_{f \in \mathscr{F}}R_{srm}(f)=min_{f \in \mathscr{F}}\frac{1}{N} \sum_{i=1}^{N}L(y_i,f(x_i)) + \lambda J(f) \tag{13}
\]
如贝叶斯估计中的最大后验概率估计(Maximum Posterior Probability,MAP)就是结构风险最小化的一个例子.
当模型是条件概率分布,损失函数是对数函数,模型复杂度由模型的先验概率表示时,结构风险最小化(SRM)等价于最大后验概率估计(MAP).
4. 算法
统计学习问题归结为最优化问题,统计学习的算法成为求解最优化问题的算法.
- 有解析式,解析求解
- 无解析式,数值计算
5. 模型评估与模型选择
5.1 训练误差与测试误差
- 基于损失函数的训练误差(training error).训练误差的大小,对判断给定的问题是不是一个容易学习的问题是有意义的,但本质上不重要.
- 基于模型的测试误差(test error).测试误差反映了学习方法对未知的测试数据集的预测能力,测试误差小的方法通常有更好的预测能力(也称泛化能力generralization ability),是更有效的方法.
Remarks:学习时具体采用的损失函数未必是评估时使用的损失函数.当然,让二者一致是比较理想的.
- 训练误差是学习到的模型$ \widehat{Y}=\widehat{f}(X) $ 关于训练集的平均损失:
\[
R_{emp}(\widehat{f})=\frac{1}{N} \sum_{i=1}^{N}L(y_i,\widehat{f}(x_i)) \tag{14}
\]
- 测试误差是学习到的模型$ \widehat{Y}=\widehat{f}(X) $ 关于测试集的平均损失:
\[
e_{test}(\widehat{f})=\frac{1}{M} \sum_{i=1}^{M}L(y_i,\widehat{f}(x_i)) \tag{15}
\]
e.g. 当损失函数是0/1损失时,测试误差就变成了常见的测试数据集上的误差率(error rate)
\[
e_{test}(\widehat{f})=\frac{1}{M} \sum_{i=1}^{M}I(y_i \ne \widehat{f}(x_i)) \tag{16}
\]
相应的,常见测试数据集上的准确率(accuracy):
\[
r_{test}(\widehat{f})=\frac{1}{M} \sum_{i=1}^{M}I(y_i = \widehat{f}(x_i)) \tag{16}
\]
显然, \[ e_{test} + r_{test} = 1\]
5.2 过拟合与模型选择
过拟合(Over-fitting):学习时选择的模型所包含的参数过多,以致于出现模型对已知数据(训练集)预测很好,对未知数据预测很差的现象.
多项式拟合的例子(P27)说明:当模型的复杂度增大时,训练误差会逐渐减小并趋向0;而测试误差会先减小后增大.当选择的模型复杂度过大,过拟合的现象就会发生.
5.3 正则化与交叉验证
- 正则化(Regularization):正则化是结构风险最小化策略的实现,是经验风险加上一个正则化项或罚项,正则化项一般是模型复杂度的单调递增函数,比如模型参数向量的范数.
e.g.:回归问题中,损失函数是平方损失,正则化项可以是参数向量的$ L_2 $范数.
\[L(w)=\frac{1}{N} \sum_{i=1}^{N}(f(x_i;w)-y_i))^2 + \frac{\lambda}{2}||w||_1 \tag{17}\]
- 能够很好地解释已知数据并且十分简单才是好地模型.
- 从贝叶斯估计的角度来看,正则项对英语模型的先验概率,可以假设复杂的模型有较大的先验概率.
数据充足时,随机分层:
- training set
- validation set
- test set
数据不足时,交叉验证:重复使用数据,将给定的数据进行切分,将切分的数据合为训练集和测试集,在此基础上反复进行训练.
- 简单交叉验证:(70%training set,30%test set)
- S-fold cross validation:随机分成S个互不相交的大小相同的子集,S-1个用于训练,余下测试;对可能的S种组合重复选择,选出S次评测种平均测试误差最小的.
- 留一交叉验证(leave-one-out cross validation):S=N,往往数据缺乏的情况下使用.
6.泛化能力
Generalization Ability:对未知数据的预测能力.一般通过测试误差来评价.
6.1 泛化误差(generalization error)
事实上,范化误差就是所学习到的模型的期望风险.
\[
R_{exp}(\widehat{f})=E_p[L(Y,\widehat{f}(X))]= \int_\{x \times y\} L(y,\widehat{f}(x))P(x,y)dxdy \tag{18}
\]
6.2 泛化误差上界(generalization error bound)
e.g.:二分类问题的泛化误差上界
Hoeffding不等式: $ S_n=\sum_{i=1}^{n}X_i $是独立随机变量$ X_1,X_2,..,X_n $之和,$ X_i \in [a_i,b_i] $,则对任意$ t>0 $,以下不等式成立:
\[
P(S_n-E[S_n] \geqslant t) \leqslant \exp{\frac{-2t^2}{\sum_{i=1}^{n}(b_i-a_i)^2}} \tag{19}
\]
\[
P(E[S_n] - S_n \leqslant t) \geqslant \exp{\frac{-2t^2}{\sum_{i=1}^{n}(b_i-a_i)^2}} \tag{20}
\]
7. 生成模型与判别模型
- 监督学习的任务就是学习一个模型决策函数$ Y=f(X) $或条件概率分布$ P(Y|X) $
- 监督学习的方法可以分为生成方法(generative approach)和判别方法(discriminative approach)
7.1 生成模型(Generative Model)
由数据学习联合概率分布$ P(X,Y) $,然后求出条件概率分布$ P(Y|X) $.即给定X,输出Y.
\[
P(Y|X)=\frac{P(X,Y)}{P(X)}
\]
e.g.:
特点:
- 可还原出联合概率分布$ P(X,Y) $
- 收敛速度更快
- 存在隐变量时仍适用
7.2 判别模型(Discriminative Model)
直接学习决策函数$ Y=f(X) $或条件概率分布$ P(Y|X) $.对应给定的输入X,应该预测什么样的输出Y
e.g.:
- k近邻法
- 感知机
- 决策树
- 逻辑回归
- 最大熵
- 支持向量机SVM
- 提升方法
- 条件随机场
特点:
- 直接面对预测,往往准确率更高
- 可以对数据进行各种程度的抽象,定义特征并适用,简化学习问题
8.分类问题
输出变量Y是有限个离散值时,监督学习的预测问题变成分类问题.输入变量X可以是离散的,也可以是连续的.
- classifier
- prediction->classification
- class
8.1 二分类问题
- $ TP $ 将正类预测为正类
- $ FN $ 将正类预测为负类
- $ FP $ 将负类预测为正类
- $ TN $ 将负类预测为负类
- 精确率(precision) \[P=\frac{TP}{TP+FP}\]
- 召回率(recall) \[R=\frac{TP}{TP+FN}\]
- $ F_1 $值:精确率和召回率的调和平均 \[F_1=\frac{2TP}{2TP+FP+FN}\]
8.2 标注问题(tagging)
输入一个观测序列,输出一个标记序列或状态序列,是分类问题的一个推广.
9.回归问题(Regression)
用于预测输入变量X(自变量)和输出变量Y(因变量)之间的关系,等价于函数拟合.
- 一元回归和多元回归
- 线性回归和非线性回归
- 平方损失函数->最小而乘法(Least Squares)
- 应用于市场预测/产品质量管理/客户满意度/投资风险分析等
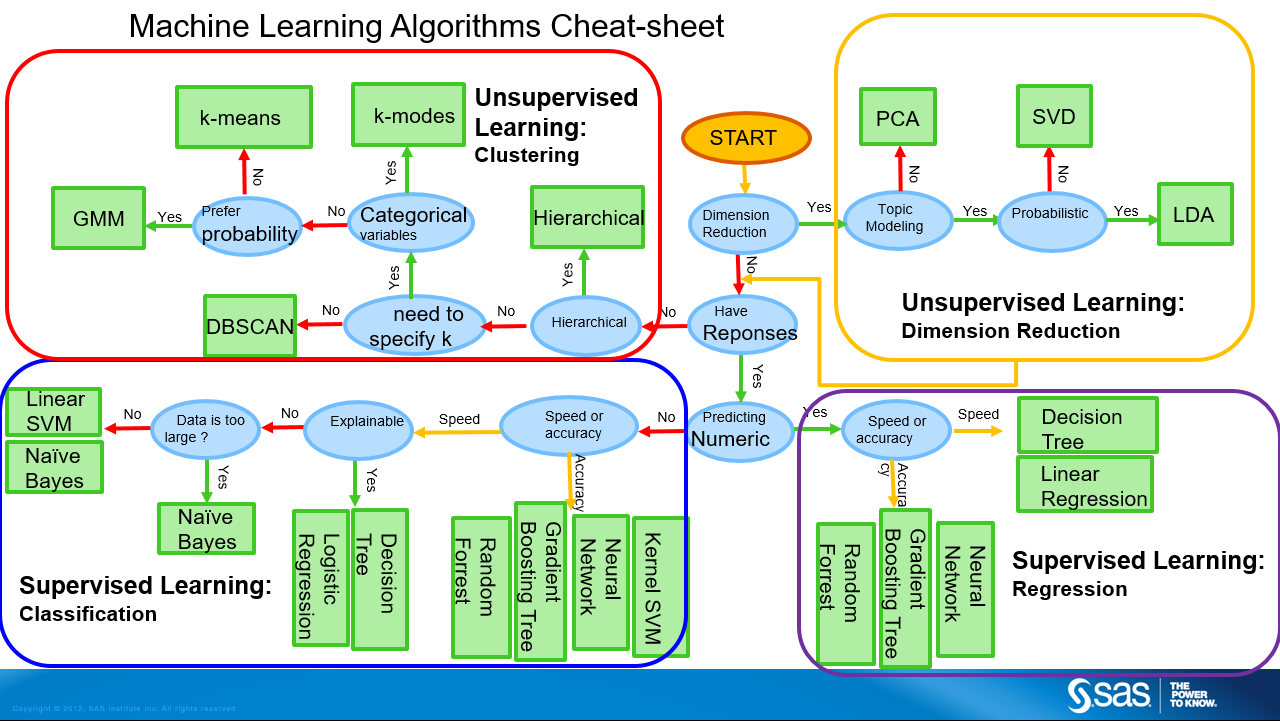
Roadmap